Introduction

We present a speech factorization approach based on a novel factorial discriminative normalization flow model (factorial DNF). Experiments conducted on a twofactor case that involves phonetic content and speaker trait demonstrates that the proposed factorial DNF has powerful capability to factorize speech signals and outperforms several comparative models in terms of information representation and manipulation.

Members

Haoran Sun, Lantian Li, Yunqi Cai, Yang Zhang, Thomas Fang Zheng, Dong Wang

Publications

Haoran Sun, Lantian Li, Yunqi Cai, Yang Zhang, Thomas Fang Zheng, Dong Wang, "Deep Generative Factorization For Speech Signal", 2020. pdf

Source Code

DNF:[1]

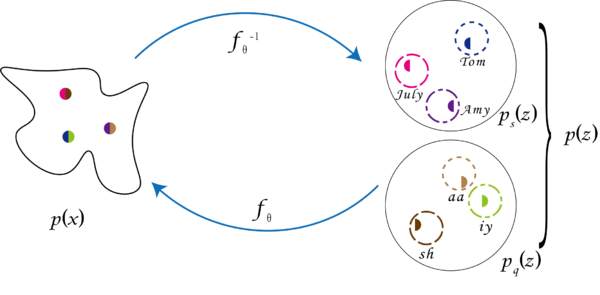
Factorial DNF

We split the latent code of DNF into several partial codes, with each partial code corresponding to a particular information factor. This model is denoted by factorial DNF. Taking the case of two information factors as an example, we split the latent code into two partial codes, z_A and z_B, corresponding to the information factor A and B respectively. Since the prior distribution is a diagonal Gaussian, z_A and z_B are naturally independent, which means:

p(z) = p(z_A)p(z_B)

We assume that the prior distributions for z_A and z_B depend on the labels corresponding to the information factors A and B, respectively. More precisely,

p(z_A) = N(z_A; µ_{yz_A(z)}; I)

p(z_B) = N(z_B; µ_{yz_B(z)}; I)

where yz_A(z) and yz_B(z) are the class labels of z for factor A and B respectively. The likelihood p(x) can therefore be written by:

log p(x) = log p(z_A) + log p(z_B) + log J(x)

Once the model has been well trained, an observation x can be encoded to z = [z_A z_B] by the invertible transform f⁻¹, and the partial codes z_A and z_B encode the information factors A and B, respectively.

Experiments

Data

The TIMIT database is used in our experiments. The original 58 phones in the TIMIT transcription are mapped to 39 phones by Kaldi toolkit following the TIMIT recipe, and 38 phones (silence excluded) are used as the phone labels. To balance the number of classes between phones and speakers, we select 20 female and 20 male speakers, resulting in 40 speakers in total.

All the speech utterances are firstly segmented into short segments according to the TIMIT phone transcriptions by force alignment. All the segments are trimmed to 200ms; if a segment is shorter than 200ms, we extend it to 200ms in both directions. All the segments are labeled by phone and speaker classes. Afterwards, every segment is converted to a 20 × 200 time-frequency spectrogram by FFT, where the window size is set to 25ms and the window shift is set to 10ms. The spectrograms are reshaped to vectors and are used as input features of deep generative models.

Encoding

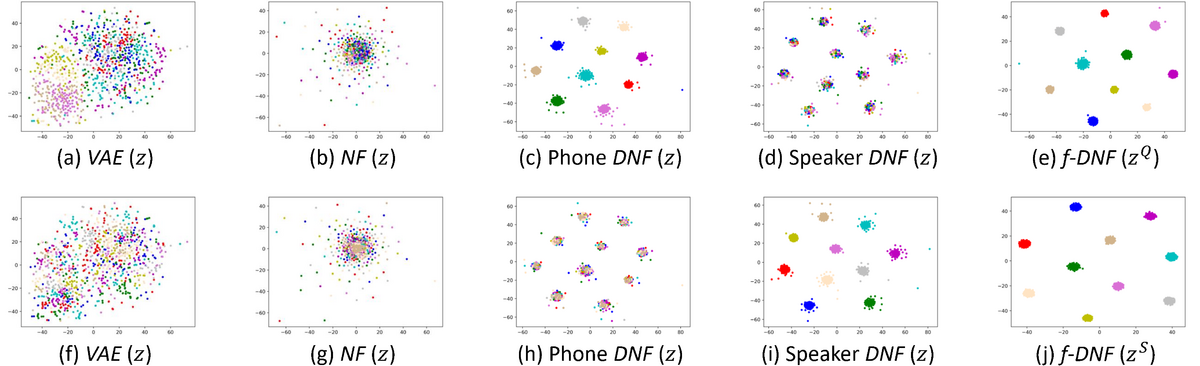
VAE and NF almost lose the class structure;

DNF can retain the class structure of the information factor corresponding to the class labels in the model training;

Factorial DNF can retain the class structure corresponding to all the information factors.

Figure: The latent codes generated by various models are as below, plotted by t-SNE.

In the first row (a) to (e), each color represents a phone; in the second row (f) to (j), each color represents a speaker.

‘Phone DNF’ denotes DNF trained with phone labels; ‘Speaker DNF’ denotes DNF trained with speaker labels.

Factor manipulation

DNF has a stronger capacity than VAE and NF to implement factor manipulation. However, the DNF-based manipulation tends to cause larger distortion on other factors. Factorial DNF has similar even better performance than DNF in terms of factor manipulation, but causes very little distortion on other factors.

We use the mean-shift approach to conduct the manipulation. Given a factor A to manipulate, we compute the mean vectors of each class on factor A, denoted by {µ_A,i}. Now for a sample x from one class c₁, we hope to change it to another class c₂. This can be obtained by moving its latent code z by a shift µ_A,c₂ − µ_A,c₁ and then transforming it back to the observation space. In summary, manipulation by the mean-shift approach is as follows:

x' = f(f⁻¹(x) + µ_A,c₂ − µ_A,c₁)

Tabel: MLP posteriors on the target class before and after phone/speaker manipulation are as below.

‘f-DNF’ denotes factorial DNF. δ(·) denotes the difference on posteriors p(·|x') and p(·|x).

                        Phone Manipulation
 Model |  p(q₂|x) | p(q₂|x') |  δ(q₂)  ||  p(s|x) |  p(s|x') |   δ(s)
  VAE  |   0.013  |  0.312   |  0.299   ||  0.612  |  0.454   |  -0.158 
  NF   |   0.013  |  0.410   |  0.397   ||  0.612  |  0.489   |  -0.123 
  DNF  |   0.013  |  0.619   |  0.606   ||  0.612  |  0.335   |  -0.277  
 f-DNF |   0.013  |  0.636  |  0.623   ||  0.612  |  0.536  |  -0.076

                        Speaker Manipulation
 Model |  p(s₂|x) | p(s₂|x') |  δ(s₂)  ||  p(q|x) |  p(q|x') |   δ(q)
  VAE  |   0.010  |  0.303   |  0.293   ||  0.520  |  0.509  |  -0.011
  NF   |   0.010  |  0.435   |  0.425   ||  0.520  |  0.484   |  -0.036 
  DNF  |   0.010  |  0.700   |  0.690   ||  0.520  |  0.349   |  -0.171  
 f-DNF |   0.010  |  0.710  |  0.700   ||  0.520  |  0.503   |  -0.017

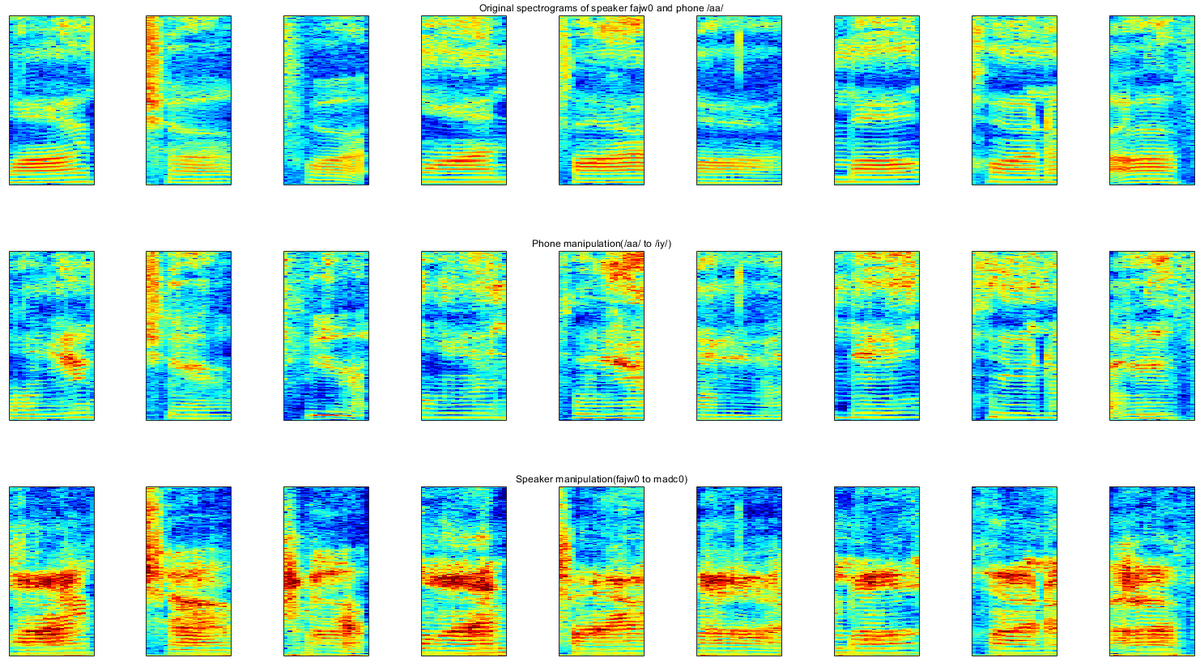
Figure: some factor manipulation examples of factorial DNF.

In the first row are original spectrograms of a female speaker fajw0 and phone /aa/.

They are converted to /iy/ while the speaker remaining the same fajw0 in the second row,

and converted to madc0 while the phone remaining the same /aa/ in the third row.

Audio: audios of a conversion sample(corresponding to the last column in the spectrograms figure).

Each audio is repeated for 10 times to make sure that it can be recognized.

The Audio before conversion

The audio after conversion from /aa/ to /iy/

The audio after conversion from fajw0 to madc0

Conclusions

We presented a speech information factorization method based on a novel deep generative model that we called factorial discriminative normalization flow. Qualitative and quantitative experimental results show that compared to all other models, the proposed factorial DNF can retain the class structure corresponding to multiple information factors, and changing one factor will cause little distortion on other factors. This demonstrates that factorial DNF can well factorize speech signal into different information factors.

Future Work

Test factorial DNF on larger datasets.
Establish general theories for deep generative factorization.

Deep Generative Factorization For Speech Signal(ICASSP21)

目录