“教学参考-12”版本间的差异
来自cslt Wiki
| 第44行: | 第44行: | ||
* 过拟合现象的根本原因在于模型记住了数据中的细枝末节,并把这些细枝末节错误地当成了规律。然而,这些规律其实并不存在,从而导致在未知数据上的性能下降。一般来说,越复杂的模型发生过拟合的可能性越大。 | * 过拟合现象的根本原因在于模型记住了数据中的细枝末节,并把这些细枝末节错误地当成了规律。然而,这些规律其实并不存在,从而导致在未知数据上的性能下降。一般来说,越复杂的模型发生过拟合的可能性越大。 | ||
* 如下图所示,一条曲线比直线在训练集上的性能更好,但发生过拟合的可能性也更大。 | * 如下图所示,一条曲线比直线在训练集上的性能更好,但发生过拟合的可能性也更大。 | ||
| + | |||
| + | |||
[[文件:Apple-orange-overfit.png]] | [[文件:Apple-orange-overfit.png]] | ||
| + | |||
| + | |||
| + | ===模型选择=== | ||
| + | * 过拟合现象的存在使得模型选择变得非常重要。复杂的模型有更强大的学习能力,同时也会带来更严重的过拟合问题,导致在实际运行时性能下降。特别是当训练数据较少时,这种过拟合更为严重。 | ||
| + | * 如何选择合适的模型呢?机器学习里有一条著名的原则:如果两个模型具有类似的性能,那么应该选择更简单的那个。这条原则称为“奥卡姆剃刀准则(Occam’s Razor)”。 | ||
| + | * 奥卡姆是个人名,英国中世纪哲学家。奥卡姆剃刀是比喻用法,意思是“删掉不必要的复杂性”。基于奥卡姆剃刀准则,在测试集上性能相近的前提下,应尽量选择那些简单的模型。例如,如果用线性模型可以解决问题,就不要选择更复杂的非线性模型;如果用10个参数的模型可以解决问题,就不要用100个参数的模型。 | ||
| + | * 所谓线性模型,是指模型的输入和输出具有线性相加关系的模型,如 y = ax1 + bx2 + cx3, 其中(x1,x2,x3)为输入变量,y为输出,y是由x1,x2,x3线性相加而得到。之所叫线性模型,是因为如果将任意一个输入(比如x1)和 y 分别作为 x轴和y轴,画出y(x)的函数,可以看到是一条直线。非线性模型是不具有这种线性关系的模型。 | ||
2022年8月2日 (二) 12:11的版本
教学目标
- 理解机器学习系统构造的基本流程:模型设计-训练-测试-选择
- 了解流程中每一步的基本原则和基本方法
- 了解数据对机器学习的重要性
教学内容
模型设计
- 没有免费的午餐: 机器学习里有很多种模型,每种模型都有其适用范围,没有哪一种模型在所有场景下都优于其他模型。这一结论在机器学习里是一条可严格证明的定理,称为“没有免费的午餐”定理。
- 机器学习实践中很重要的一点是深入理解任务场景,设计与场景匹配的模型。模型设计合理,可以极大提高学习效率,改善模型的性能。机器学习很大程度上是一种权衡的艺术
- 在模型设计中,需要考虑的因素包括:数据的格式和数据量,数据的分布形式,训练过程的内存和计算开销,可容忍的错误率,运行时的硬件能力、外部环境干扰等。在设计型时需要对这些因素综合考虑,得到最合适的建模方案。
模型训练
- 设计好了模型之后即需要对它进行学习,这一过程称为模型训练。
- 模型训练的基础方法:首先将学习目标定义成合理的数学形式,这一数学形式称为目标函数。目标函数的参数即是模型的参数。选择一个数据集(称为训练集),利用合理的优化方法来调整模型参数,使得目标函数在该训练集上的取值最大,即完成了模型训练过程。
- 以区分苹果-桔子的学习任务来举例说明。我们设计一个简单的模型: Y = a ✖ C + b ✖ S ,其中C代表颜色,S代表大小,(a,b)为待学习的模型参数。
- 收集一个训练集,集中包含若干桔子和苹果的样例,每个样例表示成(C,S,T)的形式,其中T代表水果的真实类别,T=0时代表桔子,T=1时代表苹果。我们希望Y与T越接近越好,这样就可以用Y来预测T。
- 设计一个目标函数 L=||Y-T||2。显然,L越小,说明Y和T越接近,模型越精确。因此,模型训练任务可以转化成目标函数L的最小化任务,即通过选择参数(a,b),使训练集中所有样本上计算得到L之和最小。
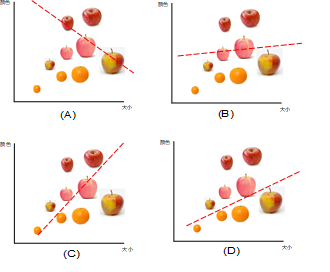
- 对目标函数求最小值可以有多种方法。右图展示了一种逐渐优化的训练过程:首先对(a,b)随机取值,然后在这一取值附近随机选择一组新的取值,如果目标函数没有增长,则丢掉该参数值,否则予以保留。这一过程重复进行,如(A) -(D)所示。经过若干次尝试后,桔子-苹果的分类面就会变得越来越准确。
优化方法:梯度下降算法
- 定义好目标函数以后,机器学习任务很大程度上转化成对目标函数L(W)的最小化任务,其中W代表模型的参数。前面我们已经提到了基于随机尝试的优化方法,但这种方法效率不高。为了更有效地完成这一优化任务,研究者提出了很多高质量的优化方法。在这些方法中,梯度下降法因其简单高效应用最为广泛。
- 如果把W想象成位置座标,L(W)的值想象成山的高度,对L(W)最小化等价于寻找到一个最深的山谷。如果函数L(W)形式比较简单,可以直接推导出使L(W)最小的W。例如,如果L=W2,则W=0即是最小值点。在实际应用中,L(W)通常很复杂,难以通过计算直接得到。这时,一般采用多步迭代算法,逐渐接近最小值。
- 想象一个人在山坡的某一个位置,他的目的是下到最低谷,怎么办呢?通常的方案是从当前位置开始向四周探索一下,然后选择一个坡度最陡、下降最快的方向迈出一步。这样一步一步走下去,就可以逐渐接近谷底。这种方法通常称为下山法(有时也叫爬山法,对应L(W)的最大化)。数学上,坡度最陡的方向称为“梯度方向”,因此这一方法也称为梯度下降法。原则上,只要我们能计算出L(W)的梯度,就可以按梯度下降法寻找到一个优化的解W。
梯度下降算法的改进
- 梯度下降法简单高效,但也存在一些问题。例如,当L(W)比较复杂时,往往呈现多个低谷,应用梯度下降法只能到达其中的某一个低谷,W的初始值不同,到达的低谷也不同。因此,算法并不能保证到达的低谷是最低的。为了解决这一问题,研究者提出一种称为模拟退火的算法,允许在下坡的时候偶尔往上坡方向也走一走,这样就可能跳出当前的低谷,到达更深的低谷。
- 梯度下降法的另一种改进是考虑山坡的起伏程度来改变前进的步长。直观上,如果山坡是弯弯曲曲的,视野不好,这时步子就要迈的小一点,否则容易错过进入山谷的机会;反之,如果山坡很平坦,哪怕坡度很大,也可以放心大胆地迈远一点,这样下山的速度会更快一些。山坡的起伏程度在数学上称为曲率,考率曲率的优化方法一般称为牛顿法。
- 除了上面这些改进,研究者们还提出了在每一步优化时随机选择训练样本子集的小批量随机梯度下降算法,研究了在参数更新时考虑前一时刻梯度的动量算法等。这些方法已经成为机器学习里的标准方法,广泛应用在各种模型的训练任务中。
模型测试
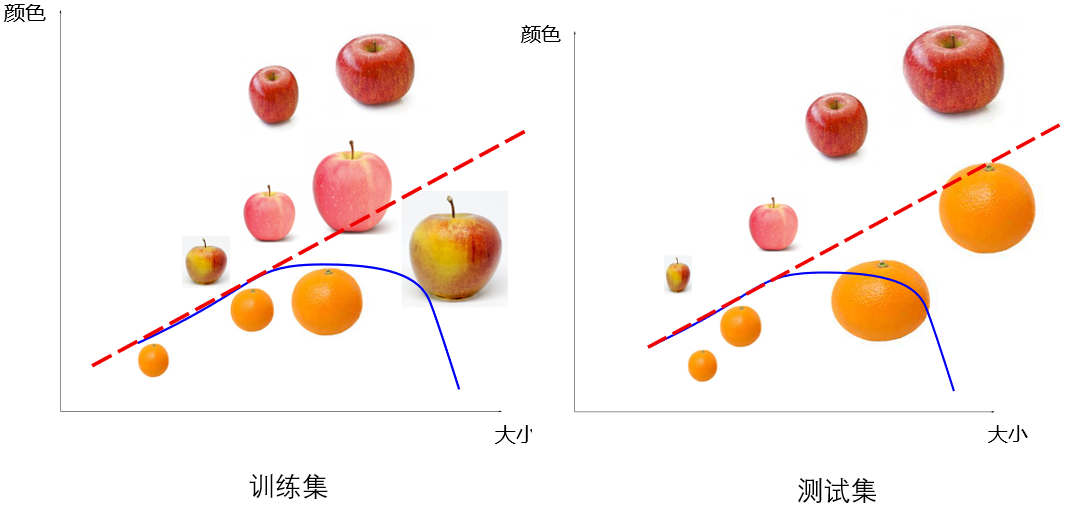
- 模型训练完成以后,需要对其性能进行测试。对模型的测试应该基于一个独立的测试集。为什么要在一个新的数据集上进行性能测试呢?这是因为模型在训练集和测试集上的性能可能存在很大差异:在训练集上性能非常好的模型,在测试集上可能会差很多。这是因为如果模型的参数和训练集中的数据过度适应,可能导致在其他数据集上性能下降。这种现象称为“过拟合”。这就如同一个只会死记硬背的学生,在课堂学习时把老师讲的所有题目都死记硬背下来,但是在考试时肯定会遇到没见过的题目,这时就做不出来了。
- 在系统测试时,我们当然更加关注它在未知数据上的表现。这是因为在实际应用中遇到的数据绝大多数是在训练集中没有出现过的未知数据。为了获知在机器学习系统的真实性能,我们需要一个独立测试集来进行性能测试。
- 过拟合现象的根本原因在于模型记住了数据中的细枝末节,并把这些细枝末节错误地当成了规律。然而,这些规律其实并不存在,从而导致在未知数据上的性能下降。一般来说,越复杂的模型发生过拟合的可能性越大。
- 如下图所示,一条曲线比直线在训练集上的性能更好,但发生过拟合的可能性也更大。
模型选择
- 过拟合现象的存在使得模型选择变得非常重要。复杂的模型有更强大的学习能力,同时也会带来更严重的过拟合问题,导致在实际运行时性能下降。特别是当训练数据较少时,这种过拟合更为严重。
- 如何选择合适的模型呢?机器学习里有一条著名的原则:如果两个模型具有类似的性能,那么应该选择更简单的那个。这条原则称为“奥卡姆剃刀准则(Occam’s Razor)”。
- 奥卡姆是个人名,英国中世纪哲学家。奥卡姆剃刀是比喻用法,意思是“删掉不必要的复杂性”。基于奥卡姆剃刀准则,在测试集上性能相近的前提下,应尽量选择那些简单的模型。例如,如果用线性模型可以解决问题,就不要选择更复杂的非线性模型;如果用10个参数的模型可以解决问题,就不要用100个参数的模型。
- 所谓线性模型,是指模型的输入和输出具有线性相加关系的模型,如 y = ax1 + bx2 + cx3, 其中(x1,x2,x3)为输入变量,y为输出,y是由x1,x2,x3线性相加而得到。之所叫线性模型,是因为如果将任意一个输入(比如x1)和 y 分别作为 x轴和y轴,画出y(x)的函数,可以看到是一条直线。非线性模型是不具有这种线性关系的模型。