“Racorn-k”版本间的差异

来自cslt Wiki
跳转至： 导航、 搜索
（→‎Experiments on several datasets）
（→‎Experiments on several datasets）
 
（相同用户的57个中间修订版本未显示）
第1行： 第1行：
 
=Project name=
 
=Project name=
−
RACORN-K: RISK-AVERSION PATTERN MATCHING-BASED PORTFOLIO SELECTION
+
RACORN-K: Risk-aversion Pattern Matching-based Portfolio Selection
  
 
=Project members=
 
=Project members=
第25行： 第25行：
  
 
==Corn-k==
 
==Corn-k==
−
 
+
Corn-k algorithm is proposed by Li et al.[1].
 
At the t-th trading period, the CORN-K algorithm first selects
 
At the t-th trading period, the CORN-K algorithm first selects
 
all the historical periods whose market status is similar to that
 
all the historical periods whose market status is similar to that
第31行： 第31行：
 
the Pearson correlation coefficient. This patten matching process
 
the Pearson correlation coefficient. This patten matching process
 
produces a set of similar periods, which we denote by C. Then do a optimization following the idea
 
produces a set of similar periods, which we denote by C. Then do a optimization following the idea
−
of BCRP[] on C. Finally, the outputs of the top-k experts that have achieved the highest accumulated return are
+
of BCRP[2] on C. Finally, the outputs of the top-k experts that have achieved the highest accumulated return are
−
weighted to derive the ensemble-based portfolio.  
+
weighted to derive the ensemble-based portfolio.
  
 
==Racorn-k==
 
==Racorn-k==
  
−
At the t-th trading period, the CORN-K algorithm first selects
+
The portfolio optimization is crucial for the success of
−
all the historical periods whose market status is similar to that
+
CORN-K. A potential problem of the existing form, however,
−
of the present market, where the similarity is measured by
+
is that the optimization is purely profit-driven. A natural idea
−
the Pearson correlation coefficient. This patten matching process
+
to consider the risk is to penalize risky portfolios when searching
−
produces a set of similar periods, which we denote by C. Then do a optimization following the idea
+
for the optimal portfolio. We use the standard deviation of log return
−
of BCRP[] on C. Finally, the outputs of the top-k experts that have achieved the highest accumulated return are
+
on C to represent the risk and subtract this term as penalty.
−
weighted to derive the ensemble-based portfolio.  
+
  
 
==Racorn(c)-k==
 
==Racorn(c)-k==
  
−
At the t-th trading period, the CORN-K algorithm first selects
+
The combination method used in CORN-K does not consider the time-variant property of the risk.
−
all the historical periods whose market status is similar to that
+
In fact, the risk of the portfolio derived from each expert tends to change quickly in an
−
of the present market, where the similarity is measured by
+
volatile market and therefore the weights of individual experts should be adjusted timely.
−
the Pearson correlation coefficient. This patten matching process
+
To achieve the quick adjustment, we use the instant return s<sub>t</sub>(w,ρ,λ) to weight the  
−
produces a set of similar periods, which we denote by C. Then do a optimization following the idea
+
experts with different λ, rather than the accumulated return.　Since s<sub>t</sub> is not available
−
of BCRP[] on C. Finally, the outputs of the top-k experts that have achieved the highest accumulated return are
+
when estimating the optimal portfolio , we approximate it by the geometric average of the returns achieved in
−
weighted to derive the ensemble-based portfolio.
+
C.
−
 
+
−
 
+
  
 
=Experiments on several datasets=
 
=Experiments on several datasets=
  
 +
We evaluate our proposed algorithm on several dataset: DJIA, MSCI, SP500(N), HSI, SP500(O).
 +
DJIA, MSCI and SP500(O) are open dataset[3] that are used in previous work. you can find it
 +
[http://olps.stevenhoi.org/ here]. To observe the performance on more recent market, we
 +
collected another two dataset: SP500(N) and HSI
 +
([http://cslt.riit.tsinghua.edu.cn/mediawiki/images/9/9d/Sp500-n_hsi.rar download]).
 +
Form the following table, we can see that our algorithm can improve Sharpe ratio and reduce
 +
maximum drawdown consistently. In most case, it can also achieve better accumulated return.
  
−
Dataset DJIA MSCI SP500(N) HSI
+
{| class="wikitable" style="margin: auto; text-align:center; width: 100%;"
−
              Criteria       RET  SR  MDD | RET  SR  MDD | RET   SR  MDD | RET   SR MDD
+
|+Performance summarization
−
---------------------------------------------------------------------------------------------------
+
|-
−
            RACORN(C)-K   0.93 0.01 0.32 | 78.38 3.73 0.21 | 12.55 0.77 0.53 | 202.04 1.60 0.28
+
|
−
Main Results  RACORN-K     0.83 -0.19 0.37 | 79.52 3.67 0.21 | 13.03  0.72 0.57 | 264.02 1.60 0.29
+
|Dataset
−
                CORN-K     0.80 -0.24 0.38 | 77.54 3.63 0.21 | 12.50  0.70 0.60 | 254.27 1.56 0.30
+
|DJIA
−
---------------------------------------------------------------------------------------------------
+
|MSCI
−
Naive Methods   UBAH       0.76 -0.43 0.39 | 0.90 0.02 0.65 | 1.52  0.24 0.50 |   3.54 0.53 0.58
+
|SP500(N)
−
                UCRP       0.81 -0.28 0.38 | 0.92 0.05 0.64 | 1.78  0.28 0.68 |   4.25 0.58 0.55
+
|HSI
−
---------------------------------------------------------------------------------------------------
+
|SP500(O)
−
Follow the       UP       0.81 -0.29 0.38 | 0.92 0.04 0.64 | 1.79  0.29 0.68 |   4.26 0.59 0.55
+
|-
−
Winner            EG       0.81 -0.29 0.38 | 0.92 0.04 0.64 | 1.75  0.28 0.67 |   4.22 0.58 0.55
+
|Criteria    
−
                  ONS       1.53 0.80 0.32 | 0.85 0.02 0.68 | 0.78 0.27 0.96 |   4.42 0.52 0.68
+
|
−
---------------------------------------------------------------------------------------------------
+
|RET  SR  MDD  
−
              ANTICOR     1.62  0.85 0.34 | 2.75 0.96 0.51 | 1.16  0.24 0.93 |   9.10 0.74 0.56
+
|RET  SR  MDD  
−
              ANTICOR2     2.28  1.24 0.35 | 3.20 1.02 0.48 | 0.71  0.22 0.97 | 12.27 0.77 0.55
+
|RET   SR  MDD  
−
Follow the      PAMR2       0.70 -0.15 0.76 | 16.73 2.07 0.54 | 0.01 -0.28 1.00 |   1.19 0.20 0.86
+
|RET   SR   MDD
−
Loser        CWMR Stdev   0.69 -0.17 0.76 | 17.14 2.07 0.54 | 0.02 -0.26 0.99 |   1.28 0.22 0.85
+
|RET  SR  MDD
−
                OLMAR1     2.53  1.16 0.37 | 14.82 1.85 0.48 | 0.03 -0.11 1.00 |   4.19 0.46 0.77
+
|-
−
                OLMAR2     1.16  0.40 0.58 | 22.34 2.08 0.42 | 0.03 -0.11 1.00 |　　3.65 0.43 0.84
+
|rowspan="3"|Main Results
−
---------------------------------------------------------------------------------------------------
+
|RACORN(C)-K
−
Pattern Matching BK       0.69 -0.68 0.43 | 2.62 1.06 0.51 | 1.97  0.31 0.59 | 13.90 0.88 0.45
+
|0.93   0.01   0.32
−
based Algorithms  BNN       0.88 -0.15 0.31 | 13.40 2.33 0.33 | 6.81  0.67 0.41 | 104.97 1.40 0.33
+
|78.38   3.73   0.21  
−
---------------------------------------------------------------------------------------------------
+
|12.55   0.77   0.53  
 +
|202.04 1.60   0.28  
 +
|7.13    1.28    0.34
 +
|-
 +
|RACORN-K
 +
|0.83 -0.19 0.37  
 +
|79.52 3.67 0.21  
 +
|13.03  0.72 0.57  
 +
|264.02 1.60 0.29  
 +
|9.27  1.33 0.32
 +
|-
 +
|CORN-K  
 +
|0.80 -0.24 0.38  
 +
|77.54 3.63 0.21  
 +
|12.50  0.70 0.60  
 +
|254.27 1.56 0.30  
 +
|8.72  1.26 0.35
 +
|-
 +
|rowspan="2"|Naive Methods
 +
|UBAH    
 +
|0.76 -0.43 0.39  
 +
|0.90 0.02 0.65  
 +
|1.52  0.24 0.50  
 +
|3.54 0.53 0.58  
 +
|1.33  0.36 0.46
 +
|-
 +
|UCRP    
 +
|0.81 -0.28 0.38  
 +
|0.92 0.05 0.64  
 +
|1.78  0.28 0.68  
 +
|4.25 0.58 0.55  
 +
|1.64  0.55 0.31
 +
|-
 +
|rowspan="3"|Follow the Winner
 +
|UP    
 +
|0.81 -0.29 0.38  
 +
|0.92 0.04 0.64  
 +
|1.79  0.29 0.68  
 +
|4.26 0.59 0.55  
 +
|1.66  0.56 0.31
 +
|-
 +
|EG    
 +
|0.81 -0.29 0.38  
 +
|0.92 0.04 0.64  
 +
|1.75  0.28 0.67  
 +
|4.22 0.58 0.55  
 +
|1.62  0.54 0.32
 +
|-
 +
|ONS    
 +
|1.53 0.80 0.32  
 +
|0.85 0.02 0.68
 +
|0.78 0.27 0.96  
 +
|4.42 0.52 0.68  
 +
|3.32 1.11 0.25
 +
|-
 +
|rowspan="6"|Follow the Loser
 +
|ANTICOR  
 +
|1.62  0.85 0.34  
 +
|2.75 0.96 0.51  
 +
|1.16  0.24 0.93  
 +
|9.10 0.74 0.56  
 +
|5.58  1.08 0.38
 +
|-
 +
|ANTICOR2  
 +
|2.28  1.24 0.35  
 +
|3.20 1.02 0.48  
 +
|0.71  0.22 0.97  
 +
|12.27 0.77 0.55  
 +
|5.86  1.01 0.49
 +
|-
 +
|PAMR2    
 +
|0.70 -0.15 0.76  
 +
|16.73 2.07 0.54  
 +
|0.01 -0.28 1.00  
 +
|1.19 0.20 0.86  
 +
|4.97 0.90 0.51
 +
|-
 +
|CWMR Stdev
 +
|0.69 -0.17 0.76  
 +
|17.14 2.07 0.54  
 +
|0.02 -0.26 0.99  
 +
|1.28 0.22 0.85  
 +
|5.92 0.96 0.51
 +
|-
 +
|OLMAR1  
 +
|2.53  1.16 0.37  
 +
|14.82 1.85 0.48  
 +
|0.03 -0.11 1.00  
 +
|4.19 0.46 0.77  
 +
|15.89 1.28 0.41
 +
|-
 +
|OLMAR2  
 +
|1.16  0.40 0.58  
 +
|22.34 2.08 0.42  
 +
|0.03 -0.11 1.00  
 +
|3.65 0.43 0.84  
 +
|9.54  1.08 0.49
 +
|-
 +
|rowspan="2"|Pattern Matching
 +
|BK    
 +
|0.69 -0.68 0.43  
 +
|2.62 1.06 0.51  
 +
|1.97  0.31 0.59  
 +
|13.90 0.88 0.45  
 +
|2.21 0.64 0.49
 +
|-
 +
|BNN    
 +
|0.88 -0.15 0.31  
 +
|13.40 2.33 0.33  
 +
|6.81  0.67 0.41  
 +
|104.97 1.40 0.33  
 +
|3.05 0.76 0.45
 +
|}
  
 
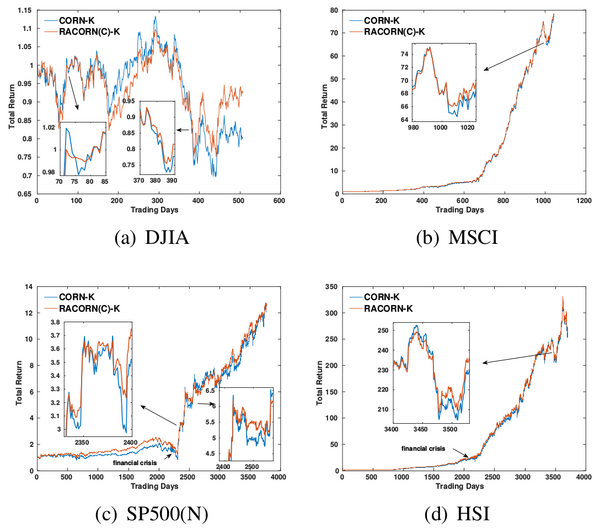
=View the impact of risk-aversion=
 
=View the impact of risk-aversion=
  
−
To verify the factorization, we can reconstruct the speech signal from the factors. The reconstruction is simply based on a DNN,
+
From RET curves we can see that RACORN(C)-K behaves more
−
as shown below.
+
‘smooth’ than CORN-K. Due to this smoothness, the risk
−
Each factor passes a unique deep neural net, the output of the three DNNs are added together, and compared with the target,
+
of the strategy is reduced, and extremely poor trading can be
−
which is the logarithm of the spectrum of the original signal. This means that the output of the DNNs of the three factors are
+
largely avoided.
−
assumed to be convolved together to produce the original speech.  
+
  
−
[[文件:fact-recover-dnn.png|500px]]
+
[[文件:Racornk-fig1.png|600px]]
  
−
Note that the factors are learned from Fbanks, by which some speech information
 
−
has been lost, however the recovery is rather successfull.
 
  
 +
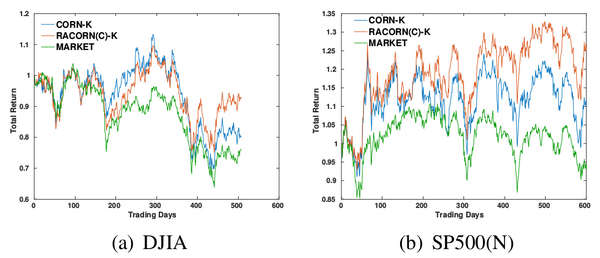
==View the impact of risk-aversion on volatile markets==
  
−
==View the reconstruction==
+
On volatile markets, our proposed algorithms are more effective.
−
 
+
−
[[文件:fact-recover.png|500px]]
+
−
 
+
  
 +
[[文件:Racornk-fig2.png|600px]]
  
 
=Reference=
 
=Reference=
  
−
[1] Lantian Li, Yixiang Chen, Ying Shi, Zhiyuan Tang, and Dong Wang, “Deep speaker feature learning for text-independent speaker verification,”, Interspeech 2017.  
+
[1] Bin Li, Steven CH Hoi, and Vivekanand Gopalkrishnan, “Corn: Correlation-driven nonparametric learning approach for portfolio selection,”, ACM Transactions on Intelligent Systems and Technology (TIST), vol. 2, no. 3,pp. 21, 2011.  
−
 
+
−
[2] Ehsan Variani, Xin Lei, Erik McDermott, Ignacio Lopez Moreno, and Javier Gonzalez-Dominguez, “Deep neural networks for small footprint text-dependent speaker
+
−
verification,”, ICASSP 2014.
+
−
 
+
−
[3] Lantian Li, Dong Wang, Yixiang Chen, Ying Shing, Zhiyuan Tang, http://wangd.cslt.org/public/pdf/spkfact.pdf
+
  
−
[4] Lantian Li, Zhiyuan Tang, Dong Wang, FULL-INFO TRAINING FOR DEEP SPEAKER FEATURE LEARNING, http://wangd.cslt.org/public/pdf/mlspk.pdf
+
[2] Thomas M Cover and David H Gluss, “Empirical bayes stock market portfolios,” Advances in applied mathematics, vol. 7, no. 2, pp. 170–181, 1986.
  
−
[5] Zhiyuan Thang, Lantian Li, Dong Wang, Ravi Vipperla "Collaborative Joint Training with Multi-task Recurrent Model for Speech and Speaker Recognition", IEEE Trans. on Audio, Speech and Language Processing, vol. 25, no.3, March 2017.
+
[3] B Li, D Sahoo, and SCH Hoi, “Olps: A toolbox for online portfolio selection,” Journal of Machine Learning Research (JMLR), 2015.
  
−
[6] Dong Wang,Lantian Li,Ying Shi,Yixiang Chen,Zhiyuan Tang., "Deep Factorization for Speech Signal", https://arxiv.org/abs/1706.01777
+
=Contact Me=
 +
Email: yang-wang16@mails.tsinghua.edu.cn

2018年3月17日 (六) 11:37的最后版本

Project name

RACORN-K: Risk-aversion Pattern Matching-based Portfolio Selection

Project members

Yang Wang, Dong Wang, Yaodong Wang, You Zhang

Introduction

Portfolio selection is the central task for assets management, but it turns out to be very challenging. Methods based on pattern matching, particularly the CORN-K algorithm, have achieved promising performance on several stock markets. A key shortage of the existing pattern matching methods, however, is that the risk is largely ignored when optimizing portfolios, which may lead to unreliable profits, particularly in volatile markets. To make up this shortcoming， We propose a risk-aversion CORN-K algorithm, RACORN-K, that penalizes risk when searching for optimal portfolios. Experiment results demonstrate that the new algorithm can deliver notable and reliable improvements in terms of return, Sharp ratio and maximum drawdown, especially on volatile markets.


Corn-k

Corn-k algorithm is proposed by Li et al.[1]. At the t-th trading period, the CORN-K algorithm first selects all the historical periods whose market status is similar to that of the present market, where the similarity is measured by the Pearson correlation coefficient. This patten matching process produces a set of similar periods, which we denote by C. Then do a optimization following the idea of BCRP[2] on C. Finally, the outputs of the top-k experts that have achieved the highest accumulated return are weighted to derive the ensemble-based portfolio.

Racorn-k

The portfolio optimization is crucial for the success of CORN-K. A potential problem of the existing form, however, is that the optimization is purely profit-driven. A natural idea to consider the risk is to penalize risky portfolios when searching for the optimal portfolio. We use the standard deviation of log return on C to represent the risk and subtract this term as penalty.

Racorn(c)-k

The combination method used in CORN-K does not consider the time-variant property of the risk. In fact, the risk of the portfolio derived from each expert tends to change quickly in an volatile market and therefore the weights of individual experts should be adjusted timely. To achieve the quick adjustment, we use the instant return st(w,ρ,λ) to weight the experts with different λ, rather than the accumulated return.　Since st is not available when estimating the optimal portfolio , we approximate it by the geometric average of the returns achieved in C.

Experiments on several datasets

We evaluate our proposed algorithm on several dataset: DJIA, MSCI, SP500(N), HSI, SP500(O). DJIA, MSCI and SP500(O) are open dataset[3] that are used in previous work. you can find it here. To observe the performance on more recent market, we collected another two dataset: SP500(N) and HSI (download). Form the following table, we can see that our algorithm can improve Sharpe ratio and reduce maximum drawdown consistently. In most case, it can also achieve better accumulated return.

Performance summarization
Dataset DJIA MSCI SP500(N) HSI SP500(O)
Criteria RET SR MDD RET SR MDD RET SR MDD RET SR MDD RET SR MDD
Main Results RACORN(C)-K 0.93 0.01 0.32 78.38 3.73 0.21 12.55 0.77 0.53 202.04 1.60 0.28 7.13 1.28 0.34
RACORN-K 0.83 -0.19 0.37 79.52 3.67 0.21 13.03 0.72 0.57 264.02 1.60 0.29 9.27 1.33 0.32
CORN-K 0.80 -0.24 0.38 77.54 3.63 0.21 12.50 0.70 0.60 254.27 1.56 0.30 8.72 1.26 0.35
Naive Methods UBAH 0.76 -0.43 0.39 0.90 0.02 0.65 1.52 0.24 0.50 3.54 0.53 0.58 1.33 0.36 0.46
UCRP 0.81 -0.28 0.38 0.92 0.05 0.64 1.78 0.28 0.68 4.25 0.58 0.55 1.64 0.55 0.31
Follow the Winner UP 0.81 -0.29 0.38 0.92 0.04 0.64 1.79 0.29 0.68 4.26 0.59 0.55 1.66 0.56 0.31
EG 0.81 -0.29 0.38 0.92 0.04 0.64 1.75 0.28 0.67 4.22 0.58 0.55 1.62 0.54 0.32
ONS 1.53 0.80 0.32 0.85 0.02 0.68 0.78 0.27 0.96 4.42 0.52 0.68 3.32 1.11 0.25
Follow the Loser ANTICOR 1.62 0.85 0.34 2.75 0.96 0.51 1.16 0.24 0.93 9.10 0.74 0.56 5.58 1.08 0.38
ANTICOR2 2.28 1.24 0.35 3.20 1.02 0.48 0.71 0.22 0.97 12.27 0.77 0.55 5.86 1.01 0.49
PAMR2 0.70 -0.15 0.76 16.73 2.07 0.54 0.01 -0.28 1.00 1.19 0.20 0.86 4.97 0.90 0.51
CWMR Stdev 0.69 -0.17 0.76 17.14 2.07 0.54 0.02 -0.26 0.99 1.28 0.22 0.85 5.92 0.96 0.51
OLMAR1 2.53 1.16 0.37 14.82 1.85 0.48 0.03 -0.11 1.00 4.19 0.46 0.77 15.89 1.28 0.41
OLMAR2 1.16 0.40 0.58 22.34 2.08 0.42 0.03 -0.11 1.00 3.65 0.43 0.84 9.54 1.08 0.49
Pattern Matching BK 0.69 -0.68 0.43 2.62 1.06 0.51 1.97 0.31 0.59 13.90 0.88 0.45 2.21 0.64 0.49
BNN 0.88 -0.15 0.31 13.40 2.33 0.33 6.81 0.67 0.41 104.97 1.40 0.33 3.05 0.76 0.45

View the impact of risk-aversion

From RET curves we can see that RACORN(C)-K behaves more ‘smooth’ than CORN-K. Due to this smoothness, the risk of the strategy is reduced, and extremely poor trading can be largely avoided.

Racornk-fig1.png


View the impact of risk-aversion on volatile markets

On volatile markets, our proposed algorithms are more effective.

Racornk-fig2.png

Reference

[1] Bin Li, Steven CH Hoi, and Vivekanand Gopalkrishnan, “Corn: Correlation-driven nonparametric learning approach for portfolio selection,”, ACM Transactions on Intelligent Systems and Technology (TIST), vol. 2, no. 3,pp. 21, 2011.

[2] Thomas M Cover and David H Gluss, “Empirical bayes stock market portfolios,” Advances in applied mathematics, vol. 7, no. 2, pp. 170–181, 1986.

[3] B Li, D Sahoo, and SCH Hoi, “Olps: A toolbox for online portfolio selection,” Journal of Machine Learning Research (JMLR), 2015.

Contact Me

Email: yang-wang16@mails.tsinghua.edu.cn

取自“http://cslt.org/mediawiki/index.php?title=Racorn-k&oldid=29903”